欧拉函数,解析数论中的互质计数与性质

揭秘数学界的“万能钥匙”——欧拉函数

亲爱的数学爱好者们，你是否曾在数学的海洋中迷失方向，被那些复杂的公式和定理搞得头昏脑胀？别担心，今天我要给大家介绍一位数学界的“万能钥匙”——欧拉函数。它就像一位神奇的向导，能帮你轻松解开数学难题，让我们一起走进欧拉函数的奇妙世界吧！

一、欧拉函数的诞生

在遥远的18世纪，有一位名叫莱昂哈德·欧拉的数学家，他不仅才华横溢，而且对数学有着浓厚的兴趣。有一天，他在研究数学问题时，突然灵感迸发，发明了一个神奇的函数——欧拉函数。从此，欧拉函数成为了数学界的一颗璀璨明珠。

二、欧拉函数的定义

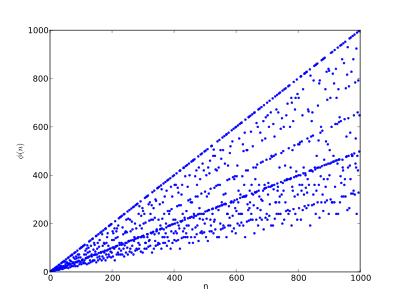
欧拉函数，用希腊字母φ表示，它描述了一个神奇的现象：对于任意正整数n，欧拉函数φ(n)表示小于n的正整数中与n互质的数的个数。所谓互质，就是指两个数的最大公约数为1。简单来说，欧拉函数就是找出与n互质的数的个数。

三、欧拉函数的性质

欧拉函数具有许多有趣的性质，下面列举几个：

1. 非负性：对于任何正实数值，欧拉函数的值都不会小于零。

2. 递增性：如果一个数的值大于零，那么它的值应该增加，而不是减少。

3. 复杂关系：欧拉函数能够表述出复杂的数学关系，比如恒定函数、线性函数和指数函数。

4. 独特性质：欧拉函数的值可以反映出所给定实数的独特性质。

四、欧拉函数的应用

欧拉函数在数学和物理学中有着广泛的应用，以下列举几个例子：

1. 求解积分问题：欧拉函数可以用来计算某一函数在一段特定区间上的积分。

2. 解决微积分问题：欧拉函数还可以被用来解决微积分问题，比如求解方程的渐进解。

3. 物理学应用：在物理学中，欧拉函数可以用来分析各种物理过程，解决带有非线性运动的问题。

4. 密码学应用：在密码学中，欧拉函数被用来构建安全的加密算法，如RSA加密算法。

五、欧拉函数的拓展

欧拉函数的研究不仅限于数学和物理学，还涉及到其他领域，如：

1. 质数分布模型：欧拉函数的研究可以帮助我们了解质数分布模型，如费马大定理、欧拉猜想以及金字塔猜想等。

2. 自然数的极限表示法：欧拉函数的研究有助于我们了解自然数的极限表示法。

3. 自变量存在性证明：欧拉函数的研究可以帮助我们证明自变量存在性。

4. 演化作用预测：欧拉函数在预测演化作用、模拟宇宙学及给出有关动力学模型的精准结果等方面也有着重要作用。

欧拉函数作为数学界的一把“万能钥匙”，在各个领域都有着广泛的应用。它不仅揭示了数学的奥秘，还为我们解决实际问题提供了有力工具。让我们一起探索欧拉函数的奇妙世界，感受数学的魅力吧！